กฎของโอห์มสำหรับห่วงโซ่ที่สมบูรณ์และส่วนของห่วงโซ่: ตัวเลือกสำหรับการเขียนสูตร คำอธิบาย และคำอธิบาย

ไม่มีทางที่ช่างไฟฟ้าหรือผู้เชี่ยวชาญด้านอิเล็กทรอนิกส์มืออาชีพจะหลีกเลี่ยงกฎของโอห์มในกิจกรรมของตนเองได้ โดยแก้ไขปัญหาใดๆ ที่เกี่ยวข้องกับการตั้งค่า การปรับแต่ง และการซ่อมแซมวงจรอิเล็กทรอนิกส์และไฟฟ้า

จริงๆ แล้วทุกคนต้องเข้าใจกฎหมายนี้ เพราะทุกคนต้องรับมือกับเรื่องไฟฟ้าในชีวิตประจำวัน

และถึงแม้ว่ากฎของโอห์มนักฟิสิกส์ชาวเยอรมันจะระบุไว้ในหลักสูตรระดับมัธยมศึกษา แต่ในทางปฏิบัติก็ไม่ได้มีการศึกษาอย่างทันท่วงทีเสมอไป ดังนั้นในเนื้อหาของเราเราจะพิจารณาหัวข้อที่เกี่ยวข้องตลอดชีวิตและทำความเข้าใจตัวเลือกในการเขียนสูตร

ส่วนเดียวและวงจรไฟฟ้าที่สมบูรณ์

เมื่อพิจารณาวงจรไฟฟ้าจากมุมมองของการใช้กฎของโอห์มกับวงจรควรสังเกตตัวเลือกการคำนวณที่เป็นไปได้สองตัวเลือก: สำหรับส่วนที่แยกจากกันและสำหรับวงจรเต็มเปี่ยม

การคำนวณกระแสของส่วนวงจรไฟฟ้า

ตามกฎแล้วส่วนของวงจรไฟฟ้าจะถือว่าเป็นส่วนหนึ่งของวงจรที่ไม่รวมแหล่งกำเนิดของ EMF เนื่องจากมีความต้านทานภายในเพิ่มเติม

ดังนั้นสูตรการคำนวณในกรณีนี้จึงดูง่าย:

ฉัน = ยู/อาร์,

โดยที่:

• ฉัน – ความแรงในปัจจุบัน
• ยู – แรงดันไฟฟ้าที่ใช้
• ร - ความต้านทาน.

การตีความสูตรนั้นง่าย - กระแสที่ไหลผ่านส่วนหนึ่งของวงจรเป็นสัดส่วนกับแรงดันไฟฟ้าที่ใช้และความต้านทานเป็นสัดส่วนผกผัน

กราฟิกที่เรียกว่า "เดซี่" ซึ่งนำเสนอรูปแบบต่างๆ ของสูตรตามกฎของโอห์มทั้งชุด เครื่องมือที่สะดวกสำหรับการจัดเก็บกระเป๋า: ภาค "P" - สูตรพลังงาน ภาค "U" - สูตรแรงดันไฟฟ้า ภาค “ฉัน” - สูตรปัจจุบัน ภาค “R” - สูตรความต้านทาน

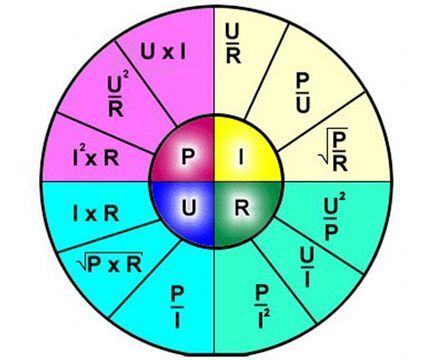
ดังนั้นสูตรจึงอธิบายอย่างชัดเจนถึงการพึ่งพากระแสไหลผ่านส่วนที่แยกต่างหากของวงจรไฟฟ้าสัมพันธ์กับค่าแรงดันและความต้านทานที่แน่นอน

สูตรนี้สะดวกในการใช้งานเช่นเมื่อคำนวณพารามิเตอร์ของความต้านทานที่ต้องบัดกรีเข้าไปในวงจรหากได้รับแรงดันและกระแส

กฎของโอห์มและผลที่ตามมาสองประการที่วิศวกรไฟฟ้าเครื่องกลมืออาชีพ วิศวกรไฟฟ้า วิศวกรอิเล็กทรอนิกส์ และใครก็ตามที่เกี่ยวข้องกับการทำงานของวงจรไฟฟ้าทุกคนต้องรู้ จากซ้ายไปขวา: 1 - การกำหนดปัจจุบัน; 2 - การกำหนดความต้านทาน; 3 - คำจำกัดความของแรงดันไฟฟ้าโดยที่ I - กระแส, U - แรงดัน, R - ความต้านทาน

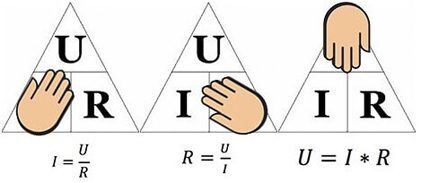
รูปด้านบนจะช่วยกำหนด เช่น กระแสที่ไหลผ่านความต้านทาน 10 โอห์ม ซึ่งใช้แรงดันไฟฟ้า 12 โวลต์ แทนที่ค่าต่างๆ เราพบว่า – I = 12/10 = 1.2 แอมแปร์

ปัญหาในการค้นหาความต้านทาน (เมื่อทราบกระแสและแรงดัน) หรือแรงดันไฟฟ้า (เมื่อทราบแรงดันและกระแส) ได้รับการแก้ไขในลักษณะเดียวกัน

ดังนั้นคุณสามารถเลือกแรงดันไฟฟ้าในการทำงานที่ต้องการ ความแรงกระแสที่ต้องการ และองค์ประกอบต้านทานที่เหมาะสมที่สุดได้ตลอดเวลา

สูตรที่เสนอให้ใช้ไม่จำเป็นต้องคำนึงถึงพารามิเตอร์ของแหล่งจ่ายแรงดันไฟฟ้าอย่างไรก็ตาม วงจรที่มี เช่น แบตเตอรี่ จะถูกคำนวณโดยใช้สูตรอื่น ในแผนภาพ: A – การเปิดแอมป์มิเตอร์; V - เปิดโวลต์มิเตอร์

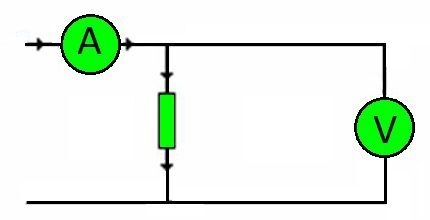
อย่างไรก็ตามสายเชื่อมต่อของวงจรใด ๆ นั้นเป็นความต้านทาน จำนวนโหลดที่ต้องรับจะพิจารณาจากแรงดันไฟฟ้า

ด้วยเหตุนี้ เมื่อใช้กฎของโอห์มอีกครั้ง จึงสามารถเลือกหน้าตัดของตัวนำที่ต้องการได้อย่างแม่นยำ ทั้งนี้ขึ้นอยู่กับวัสดุแกนกลาง

เรามีคำแนะนำโดยละเอียดบนเว็บไซต์ของเรา การคำนวณหน้าตัดของสายเคเบิล ในแง่ของกำลังและกระแส

ตัวเลือกการคำนวณสำหรับห่วงโซ่ที่สมบูรณ์

วงจรที่สมบูรณ์ประกอบด้วยส่วน (ส่วน) รวมถึงแหล่งกำเนิดของ EMF นั่นคือในความเป็นจริงแล้ว ความต้านทานภายในของแหล่งกำเนิด EMF จะถูกเพิ่มให้กับส่วนประกอบตัวต้านทานที่มีอยู่ของส่วนวงจร

ดังนั้นจึงสมเหตุสมผลที่จะเปลี่ยนสูตรข้างต้นเล็กน้อย:

ฉัน = คุณ / (R + r)

แน่นอนว่าค่าความต้านทานภายในของ EMF ในกฎของโอห์มสำหรับวงจรไฟฟ้าที่สมบูรณ์นั้นถือว่ามีค่าเล็กน้อย แม้ว่าค่าความต้านทานนี้จะขึ้นอยู่กับโครงสร้างของแหล่งกำเนิด EMF เป็นหลัก

อย่างไรก็ตามเมื่อคำนวณวงจรอิเล็กทรอนิกส์ที่ซับซ้อน วงจรไฟฟ้าที่มีตัวนำหลายตัว การมีความต้านทานเพิ่มเติมเป็นปัจจัยสำคัญ

สำหรับการคำนวณภายใต้สภาวะของวงจรไฟฟ้าที่สมบูรณ์ ค่าความต้านทานของแหล่งกำเนิด EMF จะถูกนำมาพิจารณาเสมอ ค่านี้จะถูกรวมเข้ากับความต้านทานของวงจรไฟฟ้าเอง ในแผนภาพ: I - กระแสไหล; R—องค์ประกอบต้านทานภายนอก r คือปัจจัยต้านทานของ EMF (แหล่งพลังงาน)

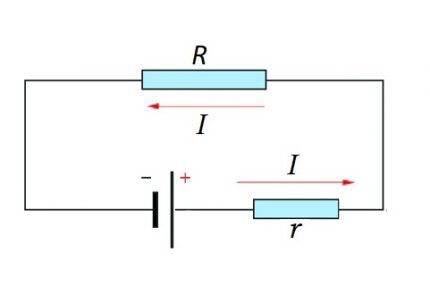
ทั้งสำหรับส่วนของวงจรและสำหรับวงจรที่สมบูรณ์ ควรคำนึงถึงโมเมนต์ธรรมชาติด้วย - การใช้กระแสคงที่หรือกระแสแปรผัน

หากพิจารณาประเด็นที่ระบุไว้ข้างต้นซึ่งเป็นลักษณะของกฎของโอห์มจากมุมมองของการใช้กระแสตรงดังนั้นกระแสสลับทุกอย่างจึงดูแตกต่างออกไปบ้าง

การพิจารณาถึงผลกระทบของกฎหมายต่อปริมาณแปรผัน

แนวคิดเรื่อง "ความต้านทาน" ต่อสภาวะของกระแสสลับที่ผ่านควรได้รับการพิจารณาเหมือนกับแนวคิดเรื่อง "อิมพีแดนซ์" มากกว่า นี่หมายถึงการรวมกันของโหลดตัวต้านทาน (Ra) และโหลดตัวต้านทานรีแอกทีฟ (Rr)

ปรากฏการณ์ดังกล่าวเกิดจากพารามิเตอร์ขององค์ประกอบอุปนัยและกฎของการสลับที่สัมพันธ์กับค่าแรงดันไฟฟ้าที่แปรผัน - ค่ากระแสไซน์ซอยด์

นี่คือวงจรสมมูลของวงจรไฟฟ้ากระแสสลับสำหรับการคำนวณโดยใช้สูตรตามกฎของโอห์ม: R - ส่วนประกอบตัวต้านทาน; C เป็นองค์ประกอบ capacitive; L—องค์ประกอบอุปนัย; EMF เป็นแหล่งพลังงาน ฉัน - กระแสปัจจุบัน

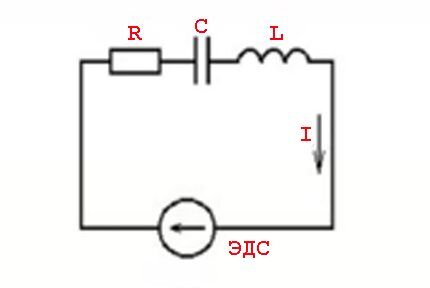
กล่าวอีกนัยหนึ่งมีผลกระทบจากค่าปัจจุบันที่นำหน้า (ความล่าช้า) จากค่าแรงดันไฟฟ้าซึ่งมาพร้อมกับการปรากฏตัวของพลังงานที่ใช้งาน (ต้านทาน) และปฏิกิริยา (อุปนัยหรือ capacitive)

ปรากฏการณ์ดังกล่าวคำนวณโดยใช้สูตร:

Z=U/ฉัน หรือ Z = R + J * (X_ล -เอ็กซ์_ค)

ที่ไหน: ซี – ความต้านทาน; ร – โหลดที่ใช้งานอยู่; เอ็กซ์_ล , เอ็กซ์_ค – โหลดอุปนัยและประจุไฟฟ้า เจ - ค่าสัมประสิทธิ์

การเชื่อมต่อองค์ประกอบแบบอนุกรมและแบบขนาน

สำหรับองค์ประกอบของวงจรไฟฟ้า (ส่วนของวงจร) จุดลักษณะเฉพาะคือการเชื่อมต่อแบบอนุกรมหรือแบบขนาน

ดังนั้นการเชื่อมต่อแต่ละประเภทจึงมาพร้อมกับรูปแบบการไหลของกระแสและการจ่ายแรงดันไฟฟ้าที่แตกต่างกันในเรื่องนี้ กฎของโอห์มก็ถูกนำไปใช้แตกต่างกันไป ขึ้นอยู่กับตัวเลือกในการรวมองค์ประกอบต่างๆ

วงจรของส่วนประกอบตัวต้านทานต่อแบบอนุกรม

ในส่วนที่เกี่ยวข้องกับการเชื่อมต่อแบบอนุกรม (ส่วนของวงจรที่มีส่วนประกอบสองส่วน) จะใช้สูตรต่อไปนี้:

• ฉัน = ฉัน₁ = ฉัน₂ ;
• ยู = ยู₁ +คุณ₂ ;
• ร = ร₁ + อาร์₂

สูตรนี้แสดงให้เห็นอย่างชัดเจนว่า กระแสที่ไหลผ่านส่วนของวงจรจะไม่เปลี่ยนแปลงค่า ไม่ว่าส่วนประกอบต้านทานจะเชื่อมต่อเป็นอนุกรมจำนวนเท่าใด

การเชื่อมต่อองค์ประกอบความต้านทานในส่วนของวงจรแบบอนุกรมเข้าด้วยกัน ตัวเลือกนี้มีกฎหมายการคำนวณของตัวเอง ในแผนภาพ: I, I1, I2 - กระแสไหล; R1, R2 - องค์ประกอบตัวต้านทาน U, U1, U2 - แรงดันไฟฟ้าที่ใช้

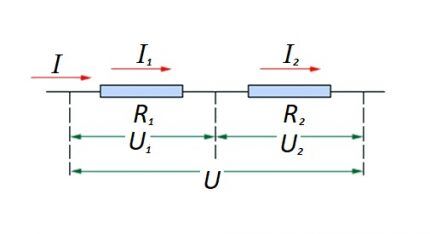
ขนาดของแรงดันไฟฟ้าที่ใช้กับส่วนประกอบต้านทานที่มีประสิทธิผลของวงจรคือผลรวมและค่ารวมของแหล่งกำเนิดแรงเคลื่อนไฟฟ้า

ในกรณีนี้ แรงดันไฟฟ้าในแต่ละส่วนประกอบจะเท่ากับ: Ux = ฉัน * Rx.

ความต้านทานรวมควรพิจารณาจากผลรวมของค่าของส่วนประกอบต้านทานทั้งหมดในวงจร

วงจรของส่วนประกอบตัวต้านทานที่เชื่อมต่อแบบขนาน

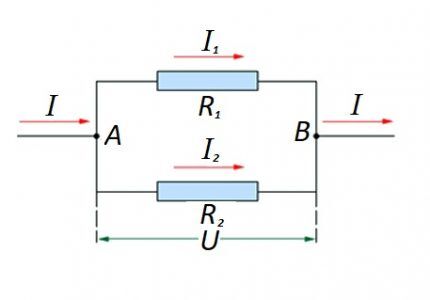
ในกรณีที่มีการเชื่อมต่อส่วนประกอบความต้านทานแบบขนาน สูตรต่อไปนี้ถือว่ายุติธรรมตามกฎของนักฟิสิกส์ชาวเยอรมัน โอห์ม:

• ฉัน = ฉัน₁ +ฉัน₂ … ;
• ยู = ยู₁ = ยู₂ … ;
• 1/ร = 1/ร₁ + 1/อาร์₂ + …

ไม่รวมตัวเลือกสำหรับการสร้างส่วนวงจรประเภท "ผสม" เมื่อใช้การเชื่อมต่อแบบขนานและแบบอนุกรม

การเชื่อมต่อองค์ประกอบความต้านทานบนส่วนของวงจรขนานกัน สำหรับตัวเลือกนี้ จะใช้กฎหมายการคำนวณอื่น ในแผนภาพ: I, I1, I2 - กระแสไหล; R1, R2 - องค์ประกอบตัวต้านทาน U คือแรงดันไฟฟ้าที่ให้มา A, B - จุดเข้า/ออก

สำหรับตัวเลือกดังกล่าว การคำนวณมักจะดำเนินการโดยการคำนวณพิกัดความต้านทานของการเชื่อมต่อแบบขนานในขั้นต้น จากนั้นค่าของตัวต้านทานที่เชื่อมต่อแบบอนุกรมจะถูกบวกเข้ากับผลลัพธ์ที่ได้รับ

รูปแบบที่เป็นส่วนประกอบและส่วนต่างของกฎหมาย

จุดทั้งหมดข้างต้นพร้อมการคำนวณใช้ได้กับเงื่อนไขเมื่อใช้ตัวนำของโครงสร้าง "เนื้อเดียวกัน" ในวงจรไฟฟ้า

ในขณะเดียวกัน ในทางปฏิบัติ เรามักจะต้องจัดการกับการสร้างแผนงาน ซึ่งโครงสร้างของตัวนำเปลี่ยนแปลงไปในส่วนต่างๆ ตัวอย่างเช่นใช้สายไฟที่มีหน้าตัดที่ใหญ่กว่าหรือในทางกลับกันลวดที่เล็กกว่าที่ทำจากวัสดุที่แตกต่างกัน

เพื่อคำนึงถึงความแตกต่างดังกล่าว มีการเปลี่ยนแปลงของสิ่งที่เรียกว่า "กฎของโอห์มดิฟเฟอเรนเชียล-อินทิกรัล" สำหรับตัวนำที่มีขนาดเล็ก ระดับความหนาแน่นกระแสจะคำนวณขึ้นอยู่กับแรงดันไฟฟ้าและค่าการนำไฟฟ้า

สูตรต่อไปนี้ใช้สำหรับการคำนวณส่วนต่าง: เจ = ό * จ

สำหรับการคำนวณอินทิกรัล สูตรคือ: ฉัน * R = φ1 – φ2 + έ

อย่างไรก็ตาม ตัวอย่างเหล่านี้ค่อนข้างใกล้เคียงกับโรงเรียนคณิตศาสตร์ชั้นสูงมากกว่า และไม่ได้นำไปใช้จริงในการปฏิบัติงานจริงของช่างไฟฟ้าธรรมดา

บทสรุปและวิดีโอที่เป็นประโยชน์ในหัวข้อ

การวิเคราะห์กฎของโอห์มโดยละเอียดในวิดีโอด้านล่างจะช่วยรวบรวมความรู้ไปในทิศทางนี้ในที่สุด

บทเรียนวิดีโอที่ไม่ซ้ำใครช่วยเสริมการนำเสนอที่เป็นลายลักษณ์อักษรเชิงทฤษฎี:

งานของช่างไฟฟ้าหรือกิจกรรมของวิศวกรอิเล็กทรอนิกส์มีความเชื่อมโยงอย่างบูรณาการกับช่วงเวลาที่เราต้องปฏิบัติตามกฎของ Georg Ohm จริงๆ นี่คือความจริงบางประการที่มืออาชีพทุกคนควรรู้

ไม่จำเป็นต้องมีความรู้ที่กว้างขวางเกี่ยวกับปัญหานี้ - เพียงการเรียนรู้ถ้อยคำหลักสามรูปแบบก็เพียงพอที่จะนำไปใช้ในทางปฏิบัติได้สำเร็จ

คุณต้องการเสริมเนื้อหาข้างต้นด้วยความคิดเห็นอันมีค่าหรือแสดงความคิดเห็นของคุณ? กรุณาเขียนความคิดเห็นในบล็อกด้านล่างบทความ หากคุณมีคำถามใดๆ อย่าลังเลที่จะถามผู้เชี่ยวชาญของเรา